작품개요
손글씨 이미지을 보고, 쓰여진 숫자가 어떤 숫자인지 알아내는 AI모델을 구현하는 것이 목표였습니다. 이를 위해 딥러닝 사용되는 기초적인 개념을 교재를 통해 공부해보았습니다만, 양이 상당히 많아서 결국 완성하지 못했습니다(…)
그래도, 제가 공부한 내용을 조금이나마 정리해서 올려보고자 합니다.
이미 딥러닝에 조예가 깊으신 선배님들이 보시기엔 굉장히 불편한 내용이 담겨 있을 수도 있습니다만 너그럽게 봐주시면 감사하겠습니다(_ _).
기본개념
MNIST dataset이란?
MNIST dataset
딥러닝 모델을 학습시키기 위한 손글씨 이미지를 모아둔 데이터베이스입니다. 다음과 같은 손글씨들이 각각 28x28 의 이미지로 저장되어 있습니다.

이 dataset과 딥러닝을 이용하여 AI모델을 학습시켜봅시다.
우선, 신경망(Nural network)의 기초 퍼셉트론(Perceptron)에 대해 이야기 해보겠습니다.
딥러닝은은 기계학습의 특별한 형태입니다. 딥러닝이란 목적을 달성하기 위해 우선 신경망에 대해 공부할 필요가 있었습니다.
신경망은 이름에서 유추할 수 있듯, 다음과 같이 인간의 뉴런(신경망)을 모방한 모습을 띄고 있습니다.
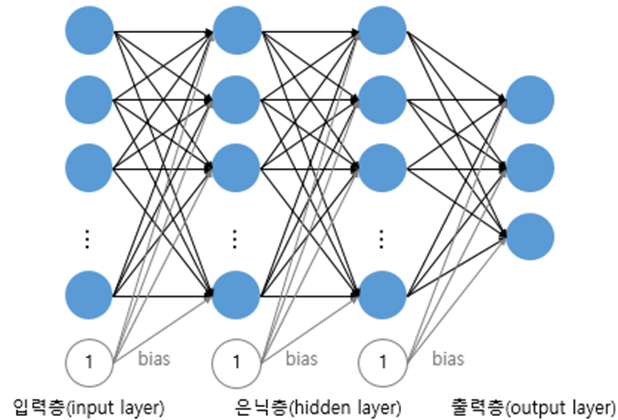
뭔가 복잡해 보이는 이것을 좀 더 간단한 형태로 살펴보면
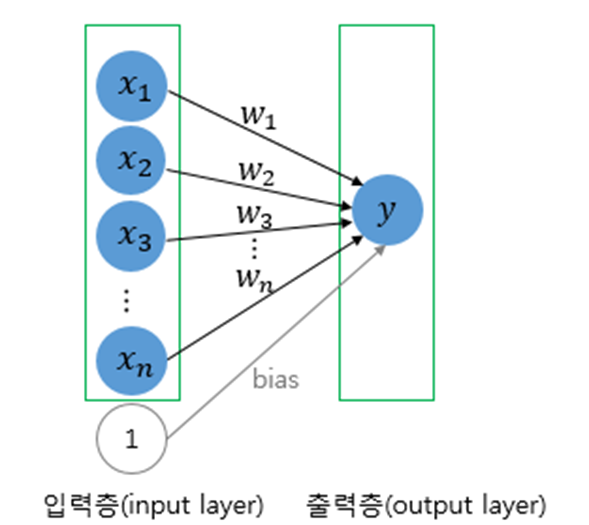
위 그림과 같습니다
위와 같은 구조를 퍼셉트론이라고 칭합니다. 퍼셉트론은 각각의 입력과 bias(편향), weight(가중치)를 이용하여 출력을 표현할 수 있습니다. 이를 통해 다양한 연산을 구현할 수 있습니다.
입력 x1, x2, x3, 편향 b와 가중치 w1, w2, w3로 이루어진 출력 y는 다음과 같이 표현할 수 있을 것입니다.
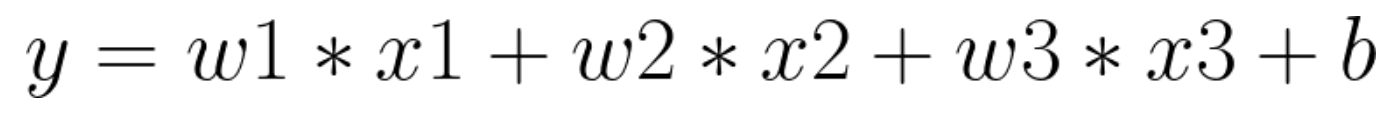
여기에 활성화 함수라는 개념을 더하여, 출력 값에 더욱 의의를 부여할 수 있게 됩니다.
대표적으로 사용되는 활성화 함수의 예는 sigmoid가 있습니다. sigmoid는 다음과 같습니다
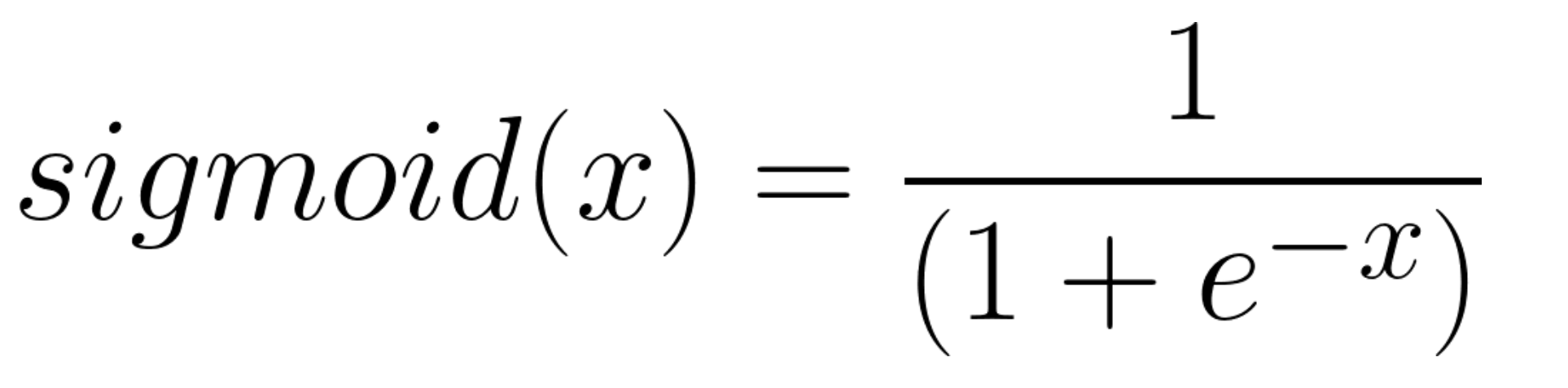
sigmoid 외에도 ReLu, softmax 등 다양한 활성화 함수가 사용됩니다.
즉, 신경망은 이런 식으로 가중치와 활성화 함수를 거친 값이 각 계층으로 전파되며, 최종적으로 출력층에 출력되는 값을 해석함으로써, 우리가 원하는 답을 얻는 구조라고 거칠게 요약할 수 있겠습니다.
출력층에 출력되는 값이 답과 얼마나 가까운지 알기 위해서 우리는 손실함수를 사용합니다. 손실 함수의 한 종류로, 오차제곱합이 있습니다.
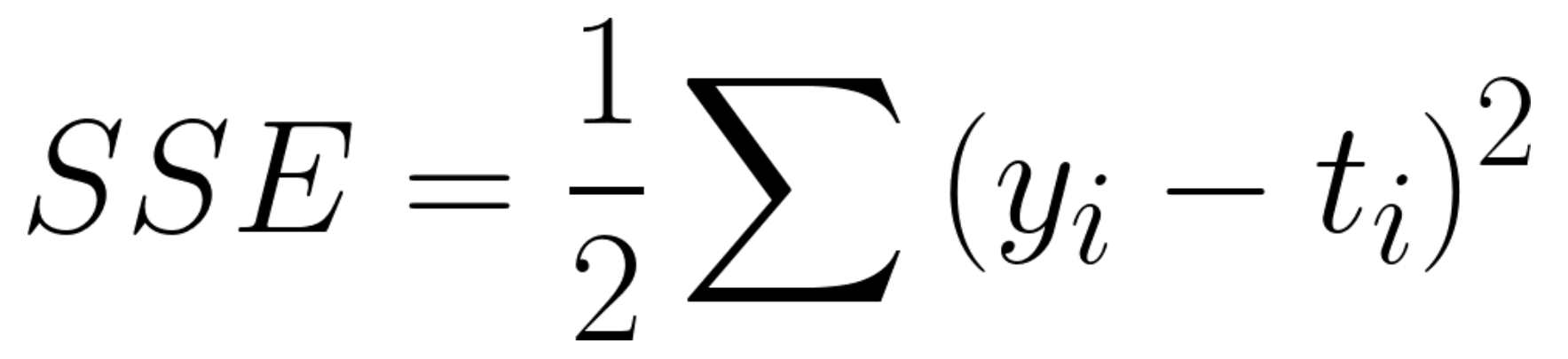
여기서 출력이 y이고, t가 정답이라고 했을 때, 위와 같은 함수를 정의함으로써 우리는 y가 t와 얼마나 차이가 나는지 (오차가 있는지) 알 수 있습니다. 예를 들자면, y1, y2, y3가 각각 입력으로 주어진 손글씨가 1, 2, 3일 확률을 나타내고, 입력으로 주어진 손글씨가 2일 때, t = [0, 1, 0]일 것입니다. 이 때 y = [0.1 , 0.8, 0.1]이라고 추정했을 경우가, y = [0.4, 0.2, 0.4]라고 추정 했을 경우보다 손실 함수 값이 작을 것입니다.
우리는 이 손실함수를 최소화하는 가중치 값들을 알아내야 합니다. 이를 위해 미분을 사용합니다
다음과 같이 가중치 값에 대해 손실함수를 미분하면, 가중치를 늘려야 할지, 줄여야 할지 알 수 있습니다. 이를 경사하강법 (gradient desent)라고 합니다. 물론 이 방법을 통해 추론한 가중치 값이 손실함수를 최소화하였는지, 단순히 극솟값을 구한 것인지는 알기 어렵습니다.
(이 문제의 해결 방법은 아직 공부하지 않아 잘 모르겠습니다. 더 공부해오겠습니다..ㅎ)
미분의 정의에 따라 가중치 값을 아주 작게 조정하여 (저는 대략 10^-4 정도의 값을 사용 했었습니다) 미분을 구현할 수도 있습니다. 다만 이러면 시간이 굉장히 오래 걸립니다. 다른 방법이 필요합니다. 이 때 오차역전파(back propagation)법을 사용할 수 있습니다.
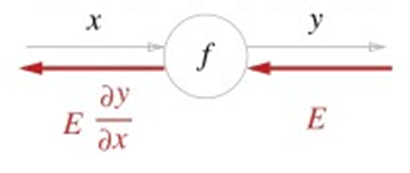
위 그림과 같이 어떤 계층을 지나갈 때, 가중치에 의한 미분 계수는 가중치를 변경하며 수치적으로 찾지 않고, chain rule을 이용하여 계층에 해당하는 도함수를 역전파함으로써 구할 수 있습니다.
이렇게 구한 미분계수에 학습률을 반영하여 가중치를 갱신할 수 있습니다. 이 과정이 경사하강법을 이용한 학습 방법입니다.
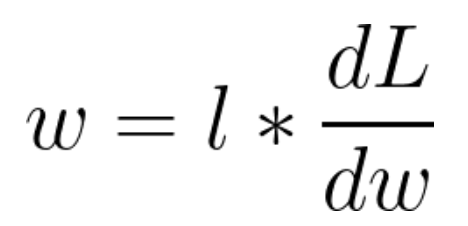
w : 가중치 , l : 학습률 , dL/dw 가중치에 대한 loss function의 변화율
학습률은 hyperparameter 중 하나로, 우리가 직접 지정해주는 parameter중 하나입니다. 학습률이 너무 낮거나 크면, 학습이 제대로 이루어지지 않을 수 있습니다.
구현
위 내용과 교재를 토대로 python code를 작성해보았습니다.
가중치가 행렬로 구현되어 있으므로, numpy를 이용해 연산하였습니다.
입력층과 은닉층 (2개의 층), 출력층으로 구성된 신경망입니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import sys, os
sys.path.append(os.pardir)
from common import *
from grad import *
from collections import OrderedDict
from layers import *
class TwoLayerNet:
def __init__(self, input_size, hidden_size,
output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# hierarchy
self.layers = OrderedDict()
self.layers['Affine1'] = \
Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = \
Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def gradient(self, x, t):
# forwardpropagation
self.loss(x, t)
# backpropagation
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# save result
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads
신경망에 사용된 계층의 구현입니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
from common import *
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx
class Relu():
def __init(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
활성화 함수의 구현입니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
def identity_function(x):
return x
def step_function(x):
return np.array(x > 0, dtype=np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def relu(x):
return np.maximum(0, x)
def relu_grad(x):
grad = np.zeros(x)
grad[x >= 0] = 1
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))
def mean_squared_error(y, t):
return 0.5 * np.sum((y - t) ** 2)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax_loss(X, t):
y = softmax(X)
return cross_entropy_error(y, t)
학습 결과
위에서 구현한 신경망을 바탕으로, data를 학습하는 code입니다.
10000개의 data에서 minibatch의 크기를 100으로 설정하였습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import numpy as np
import matplotlib.pylab as plt
from dataset.mnist import load_mnist
from twoLayer import TwoLayerNet
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# hyper_parameter
train_size = 10000
batch_size = 100
learning_rate = 0.5
iters_num = 10000
# estimate_parameter
train_loss_list = np.array([])
train_acc_list = []
test_acc_list = []
# iteration per 1epoch
iter_per_epoch = max(train_size / batch_size, 1)
print(iter_per_epoch)
print(train_size)
print(batch_size)
print(str(iter_per_epoch) + " : iter")
for i in range(iters_num):
print(str(i)+" step")
# make mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# calculate gradient
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# renew parameter
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# record results
loss = network.loss(x_batch, t_batch)
train_loss_list = np.append(train_loss_list,loss)
#print(train_loss_list[i])
# accuracy for 1 epoch
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
x = np.arange(0,iters_num,step=100)
x2 = np.arange(0,iters_num,step=iter_per_epoch)
axis1 = plt.gca()
axis1.set_xlabel('iteration')
axis2 = axis1.twinx()
axis1.plot(x, train_loss_list[x], label='los', color='blue')
axis1.set_ylabel('y1: loss')
axis2.plot(x2, train_acc_list, label='train_acc', color='orange')
axis2.plot(x2, test_acc_list, label='test_acc', color='green', linestyle='--')
axis2.set_ylabel('y2: accuracy')
axis1.legend(loc='lower left')
axis2.legend(loc='lower right')
plt.show()
1 epoch 당 학습에 사용된 train_data와 테스트에 사용된 test_data에 대해 모델의 정확도를 그래프로 나타내니 다음과 같은 결과를 얻을 수 있었습니다.
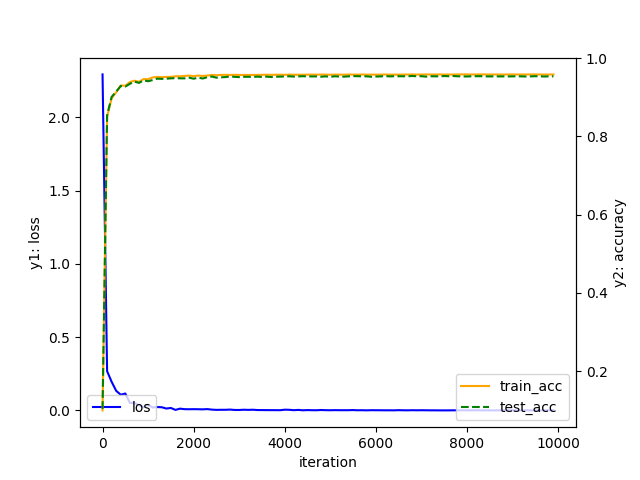
learning rate = 0.5
학습이 진행됨에 따라 loss가 줄어들고, train_data와 test_data에 대해 정확도가 함께 상승하는 것을 확인할 수 있었습니다. 학습에 사용된 train_data뿐만 아니라, 처음 보는 data인 test_data에 대해서도 모델이 유효한 것을 알 수 있습니다.
학습률에 따른 학습 효과를 확인해보기 위해 여러 학습률로도 학습을 진행해보았습니다.
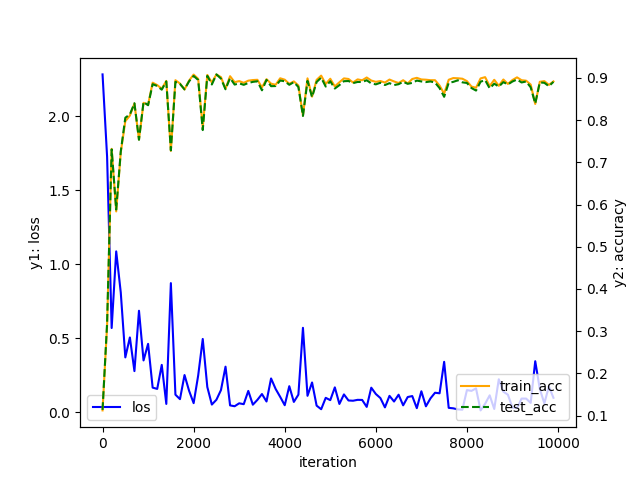
learning rate = 1.2
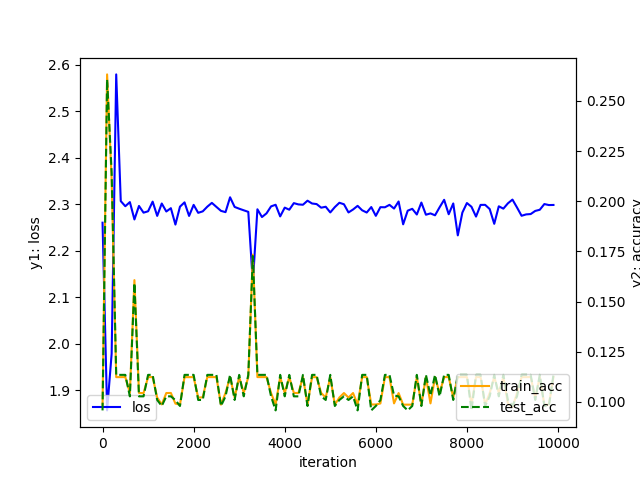
learning rate = 1.5
학습률에 따라 학습이 잘 이루어지지 않을 수도 있음을 알 수 있습니다.
마치며
내용이 많이 부실한게 느껴져서 더 준비할 수 있었으면 하는 아쉬움이 있습니다
다음엔 좀 더 고여서 오도록 하겠습니다
